Zur Vorbereitung meiner Vorlesung Statistik der Datenanalyse im Masterstudium Digitale Technologien an der FH Bielefeld habe ich heute u.a. die Vermittlung des Zentralen Grenzwertsatzes (ZGW) vorbereitet und einige Grafiken dazu in R erstellt.
Der zentrale Grenzwertsatz besagt, dass die Verteilung einer Summe Y1 + … + Yn von Zufallsvariablen für n → ∞ gegen eine Normalverteilung konvergiert. Die Zufallsvariablen Y1 , …, Yn sind unabhängig identisch verteilte Zufallsvariablen, bzw. es gibt sogar noch allgemeinere Varianten des zentralen Grenzwertsatzes, die zeigen, dass die Zufallsvariablen Y1, … , Yn sogar abhängig und verschieden verteilt sein dürfen, dabei aber keine Zufallsvariable Yi die restlichen deutlich dominieren darf.
Der ZGW begründet die herausragende Rolle der Normalverteilung in der Statistik: eine Zufallsvariable X = Y1 + … + Yn ist approximativ normalverteilt, wenn sie durch das Zusammenwirken von vielen kleinen zufälligen Effekten entsteht!
Auch liefert der ZGW eine Begründung, warum wir Hypothesentests, die auf der Annahme der Normalverteilung beruhen, durchführen können, auch wenn die ursprünglichen Variablen nicht normalverteilt sind: der Stichprobenmittelwert von n Zufallsvariablen X1, … , Xn folgt für genügend großes n einer Normalverteilung. Es wird i.d.R. n = 30 empfohlen, wobei es aber auch mit Werten n > 30 dazu kommen kann, dass noch keine Normalverteilung approximativ erreicht wurde und Hypothesentests nicht valide sind. Insbesondere bei zugrundeliegenden schiefen Verteilungen kann dieses Verhalten auftreten.
Es gibt dabei eine Vielzahl an Verteilungsformen von Daten. Im Folgenden sind exemplarisch drei Verteilungen grafisch dargestellt:
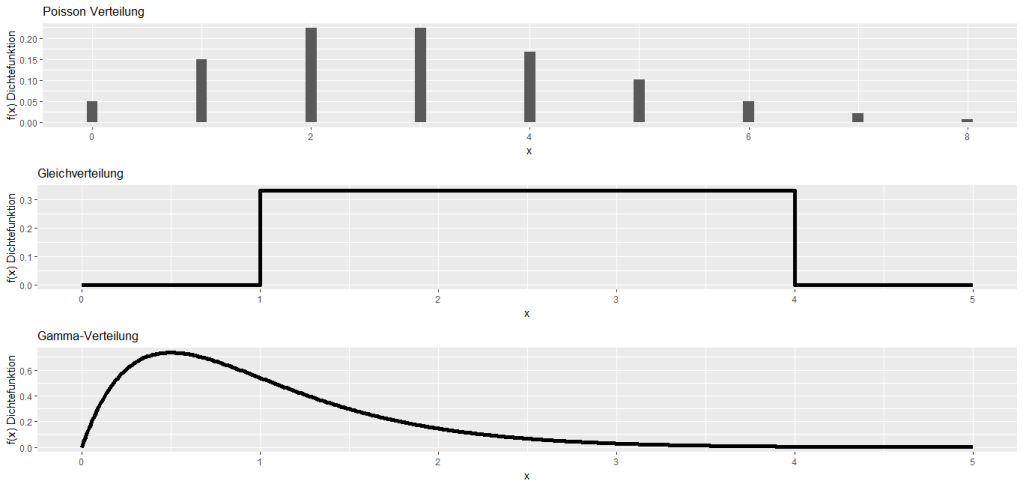
Ganz oben die Poisson Verteilung, eine Verteilung, die die Wahrscheinlichkeit der Anzahl von Ereignissen modelliert. Die Verteilung hat nur einen Parameter. Der Parameter λ gibt die durchschnittlich erwartete Häufigkeit in einem bestimmten Zeitintervall an. Daneben ist die Gleichverteilung dargestellt. Alle möglichen Zustände treten mit der gleichen Wahrscheinlichkeit auf. Im Fall von diskreten Ereignissen, z.B. beim Würfeln tritt jedes Ereignis aus der Ergebnismenge {1, 2, 3, 4, 5, 6} mit der gleichverteilten Wahrscheinlichkeit 1/6 auf. Die letzte Verteilung ist die Gamma-Verteilung. Das ist eine positive, stetige Wahrscheinlichkeitsverteilung, die zwei Parameter besitzt. Das Aussehen der Gamma-Verteilung ist durch die beiden Parameter sehr flexibel anpassbar.
Es werden im folgenden mehrmals jeweils 100 Experimente durchgeführt. Die Anzahl n, der in jedem Experiment realisierten Beobachtungen aus den Zufallsvariablen, variiert dabei von n=2, n=15, n=30 und n=50. Jedes Experiment sieht so aus, dass aus jeder der drei Verteilungen jeweils n Beobachtungen gezogen werden und dann die Summe gebildet wird. Die Histogramme stellen jetzt die 100 Summenwerte dar. Gemäß ZGW wird erwartet, dass je größer n gewählt ist, umso besser die Daten approximativ normalverteilt sind.
Für nur ein Experiment, bei dem n=2 Beobachtungen aus jeder Verteilung gezogen werden, erhalten wir beispielsweise folgende Zufallswerte (Die Befehle rpois, runif, rgamma stehen in R für random generation der jeweiligen Verteilung)
# Simulation von je 2 zufaelligen Beobachtungen in der Statistikumgebung R
x.pois <- rpois(2,3) # Parameter lambda = 3
x.unif <- runif(2,1,4) # Intervall zwischen 1 und 4
x.gamma <- rgamma(2,shape = 2,scale = 1/2) # Parameter shape = 2, scale =1/2
| Verteilung | Beobachtung 1 | Beobachtung 2 | Summe |
| Poisson | 0 | 3 | 3 |
| Gleichvert. | 3,373814 | 2,796606 | 6,17042 |
| Gamma | 1,626015 | 2,065955 | 3,691969 |
| Gesamt | 12,86239 |

Das führen wir im nächsten Schritt für n=2, n=15, n=30 und n=50 jeweils k=100 mal durch, um 100 Summen für jede Verteilung zu beobachten. Die Simulation findet innerhalb der selbstgeschriebenen Funktion my.simulation statt. Es können alle Parameter der Verteilungen und n und k im Funktionsaufruf bei Bedarf angepasst werden. Die Funktion my.simulation.plot erzeugt die Darstellung der Summenwerte als Histogramm inkl. eingefügter angepasster Normalverteilung (Mittelwert ist jeweils grün markiert).
library(ggplot2); library(ggpubr) my.simulation.plot(my.simulation(n = 2)) my.simulation.plot(my.simulation(n = 15)) my.simulation.plot(my.simulation(n = 30)) my.simulation.plot(my.simulation(n = 50))




Mit zunehmender Anzahl an Beobachtungen n fangen die Summenwerte an, approximativ einer Normalverteilung zu folgen und eine symmetrische Form anzunehmen (siehe grün eingezeichneter Mittelwert). Das gilt sowohl für Beobachtungen aus einer schiefen Verteilung (Gamma Verteilung, dritte Zeile in den Abbildungen), also auch die Summe von diskreten Zufallsvariablen (jeweils erste Zeile aus der Poisson-Verteilung).
#~~~~~~~~~~~
# Funktion zur Erzeugung der Zufallszahlen und Berechnen der Summen
#~~~~~~~~~~~
my.simulation <- function(n, k = 100,
lambda =3,
unif.min = 1, unif.max = 4,
shape = 2,scale = 1/2){
# Platzhalter fuer Ergebnisse
result <- data.frame("poisson" = 1:k,
"uniform" = 1:k,
"gamma" = 1:k,
"total" = 1:k)
for(j in 1:k){
#Poisson Verteilung Simulation n Beobachtungen
x.pois <- rpois(n,lambda)
# Speichern der Summe
result[j,"poisson"] <- sum(x.pois)
#Gleichverteilung Simulation n Beobachtungen
x.unif <- runif(n,unif.min,unif.max)
# Speichern der Summe
result[j,"uniform"] <- sum(x.unif)
#Gamma Verteilung Simulation 20 Beobachtungen
x.gamma <- rgamma(n,shape = shape,scale = scale)
# Speichern der Summe
result[j,"gamma"] <- sum(x.gamma)
# Speichern der Summe von 3 x 20 Beobachtungen aus den 3 Verteilungen
result[j,"total"] <- sum(c(x.pois, x.unif, x.gamma))
}
return(result)
}
#~~~~~~~~~~~
# Funktion zur Darstellung
#~~~~~~~~~~~
my.simulation.plot <- function(result){
## Poisson
# angepasste normalverteilte Daten
x <-seq(min(result$poisson),max(result$poisson),.1)
norm.dat.pois <- data.frame("x" = x,
"y"= dnorm(x,mean(result$poisson),sd(result$poisson)))
# histogramm
g1 <- ggplot(result, aes(x = poisson, y = stat(density) )) +
geom_histogram() +
geom_line(data = norm.dat.pois,
aes(x=x, y=y ), col= "blue", size = 1.5)+
geom_vline(xintercept = mean(result$poisson) , linetype="dashed",
color = "green", size=1.5)
## Gleichverteilung
# angepasste normalverteilte daten
x <- seq(min(result$uniform),max(result$uniform),.1)
norm.dat.unif <- data.frame(x=x, y = dnorm(x,mean(result$uniform),sd(result$uniform)))
# histogramm
g2 <- ggplot(result, aes(x = uniform, y = stat(density) )) +
geom_histogram() +
geom_line(data = norm.dat.unif,
aes(x=x, y=y ), col= "blue", size = 1.5) +
geom_vline(xintercept = mean(result$uniform) , linetype="dashed",
color = "green", size=1.5)
## Gamma
g3 <- ggplot(result, aes(x = gamma, y = stat(density) )) +
geom_histogram() +
geom_line(data = data.frame("x2"<-seq(min(result$gamma),max(result$gamma),.1),
"y2"= dnorm(x2,mean(result$gamma),sd(result$gamma))),
aes(x=x2, y=y2 ), col= "blue", size = 1.5)+
geom_vline(xintercept = mean(result$gamma) , linetype="dashed",
color = "green", size=1.5)
## multiple plots
figure <- ggarrange(g1, g2, g3,
ncol = 1, nrow = 3)
return(figure)
}
